Матричный подход
Прежде, чем мы приступим к рисованию в пространстве, нам предстоит поговорить о некоторых важных вещах, обойти которые невозможно, хотя они напрямую, казалось бы, и не связаны с программированием.
Вкратце повторим подходы, используемые нами в предыдущих главах, посвященных Direct3D. Буфер вершин заполняется данными некоторого формата об опорных вершинах, образующих примитивы. Если примитивы должны перемещаться по экрану, буфер вершин заполняется новыми данными. Для поворота объекта надо запереть буфер, чтобы получить доступ к его содержимому, и заполнить буфер новыми данными.
В трехмерных построениях мы будем избегать такого подхода. Использованные нами ранее форматы данных о вершинах содержат три пространственные координаты, и нетрудно догадаться, что для перехода к трехмерной графике надо для начала задействовать Z-координату, ранее нами игнорируемую. Конечно, потребуются еще некоторые действия, но интуиция подсказывает, что для рисования, например, кубика, надо построить треугольники, образующие стороны куба, манипулируя значением третьей координаты. А для того, чтобы нарисовать вращающийся кубик, следует периодически обновлять содержимое буфера вершин. Но мы сразу же должны оговориться, что было бы лучше, если бы мы один раз заполняли буфер данными о кубике, а воспроизводили его каждый раз немного повернутым относительно предыдущего положения. Конечно, это оптимально: заполнить буфер один раз массивом данных об объектах сцены, а при воспроизведении каждого объекта выполнять менее требовательные к ресурсам операции, указывая его текущее положение в пространстве. К такому порядку действий мы и будем стремиться. Не использовал я такого подхода раньше только потому, что боялся нагрузить вас обилием материала (этого я боюсь и сейчас), и хотел бы, чтобы мы двигались шаг за шагом. Но, к сожалению, сейчас нам придется сделать очень большой скачок, и для того, чтобы не споткнуться, следует утроить внимание. Начнем.
При описании объекта, заполнении буфера вершин опираемся на мировую систему координат. Иными словами, указываем координаты вершин объектов так, как будто все они находятся в точке начала глобальной системы координат.
Объекты трехмерной сцены наделяются системой координат, первоначально совпадающей с мировой системой. Каждая трансформация системы координат, связанной с объектом, приведет к трансформации объекта. Если перед воспроизведением объекта сместить его систему координат, то объект будет рисоваться на новом месте, т. е. относительно смещенной по одной или нескольким осям системы координат. Для осуществления поворота объекта поворачиваем систему координат, связанную с ним, вокруг одной из осей. Если на сцене присутствует несколько объектов, то перед рисованием каждого из них трансформируем систему координат, ассоциированную с этим объектом.
Надеюсь, пока все понятно и просто, и мы можем поговорить о том, как собственно осуществлять манипуляции с системой координат объекта. Самыми популярными математическими методами для описания таких преобразований служат векторный и матричный. Трехмерная графика базируется, как правило, на матричном подходе, заключающемся в том, что операции с системой координат основываются на матричном представлении. Базовым элементом матричного метода является матрица (таблица чисел) размером 4x4. Я знаю первый вопрос, который возникает всегда и у всех, кто впервые слышит о матричном методе: почему размер матрицы именно такой. В математике для описания точки в пространстве используется четыре числа, вспомогательной характеристике можно придать любой смысл, это может быть, например, заряд частицы или материальная масса. В графике четвертый компонент координаты точки называется W-координатой и предназначен для осуществления проекции точки на плоскость экрана. Это весовой фактор, на который умножаются координаты точки при ее проецировании. Его значение задается единичным.
Основной операцией, к которой прибегают при манипуляции с матрицами, является перемножение матриц, осуществляемое по формуле:

Количество строк перемножаемых матриц должно быть одинаковым.
При умножении матрицы на вектор первым множителем слагаемых суммы берутся последовательно элементы единственного столбца вектора.
Единичная матрица, т. е. матрица, по главной диагонали которой располагаются единицы, а все остальные элементы равны нулю, соответствует мировой системе координат. Другое название такой матрицы - матрица идентичности, после умножения ее на вектор получается исходный вектор.
Матрицы сдвига по осям X, Y и Z выглядят так:

Если умножить вектор (X, У, Z, W) на матрицу сдвига по оси X, в результате получится вектор (X + W o a, Y, Z, W). Умножение вектора координат всех точек объектов на матрицу сдвига приводит к перемещению объекта по нужной оси.
Три матрицы сдвига можно объединить в одну, дающую возможность осуществлять сдвиг одновременно по нескольким осям. Последняя строка такой матрицы имеет ненулевые значения в столбцах, соответствующих нужным осям.
Возвращаясь в Direct3D, поясню: у объекта устройства есть метод, позволяющий задать матрицу, на которую будут умножаться векторы координат вершин непосредственно перед отображением в пространстве. И пока в качестве такой матрицы указана матрица сдвига, все воспроизводимые объекты будут сдвигаться в пространстве.
Аналогично сдвигу, операции поворота описываются матрицами. Для поворота на угол а вокруг оси X вектор координат вершины надо умножить на такую матрицу:

Если же надо повернуть на угол (3 вокруг оси Y, то пользуются такой матрицей:

И последняя ситуация с поворотом: угол у, поворот вокруг оси Z:

Чтобы осуществить одновременный поворот по нескольким осям либо скомбинировать поворот и сдвиг, надо применить в качестве трансформаций произведение нужных матриц. При этом важен порядок, в котором мы перемножаем матрицы, он определяет последовательность трансформаций системы координат.
Операции с объектами осуществляются в трехмерном пространстве, описываемом матрицей, которую будем называть мировой матрицей. Помимо мировой матрицы требуется указать видовую матрицу, соответствующую позиции глаза наблюдателя и направлению, в котором он смотрит. В принципе, ее можно задавать точно так же, как и мировую, используя матрицы сдвига и поворота.
Последняя матрица, которая нужна для получения проекции трехмерной сцены на экране, так и называется - матрицей проекции. Значения элементов этой матрицы задают правила, согласно которым будет осуществляться проецирование: положение задней и передней отсекающих плоскостей, искажения, имитирующие перспективу (рис. 9.1).
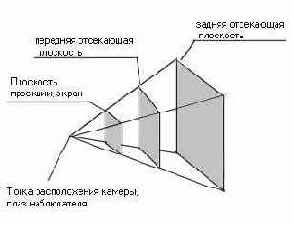
Рис. 9.1, Область видимости задается положением двух отсекающих плоскостей
Объекты, или части объектов, располагающиеся за пределами области видимости, на экран проецироваться не будут, и мы их не увидим.
Итак, мы бросили беглый взгляд на сухой теоретический материал, из которого вынесли тяжелое подозрение, что впереди нас ожидает бурелом кодирования математических формул. Отчасти это правда. Direct3D оставил программисту тяготы перемножения матриц, ожидая от него три результирующие матрицы трансформаций. Однако мы воспользуемся модулем Dxcutiis, который содержит набор полезных функций. Автор переноса на Delphi кода этих функций указан в заголовке модуля.
В списке подключаемых модулей первого примера этой главы, проекте каталога Ex01, как раз и добавлен указанный модуль. Пример очень простой, в пространстве вращаются два объекта: разноцветный треугольник и желтый квадрат (рис. 9.2).

Рис. 9.2. Простейший пример трехмерного построения фигур
Чтобы при вращении примитивов мы могли видеть обе их стороны, режим отсечения отключается, а для использования окрашенных примитивов запрещена работа с источником света:
with FDBDDevice do begin
SetRenderState(D3DRS_CULLMODE, D3DCULL_HONE);
SetRenderState(D3DRS_LIGHTING, DWORD (False)); end;
Буфер вершин запирается один раз. Семь вершин содержат координаты треугольника и квадрата. Если бы они выводились не трансформируемыми, то накладывались бы друг на друга:
Vertices.X := 0.0; // Первая вершина треугольника
Vertices.Y := 1.0;
Vertices.Z := 0.0;
Vertices.Color := $00FF0000;
Inc(Vertices);
Vertices.X := 1.0; // Вторая вершина треугольника
Vertices.Y := -1.0;
Vertices.Z := 0.0;
Vertices.Color := $0000FF00;
Inc(Vertices);
Vertices.X := -1.0; // Третья вершина треугольника
Vertices.Y := -1.0;
Vertices.Z := 0.0;
Vertices.Color := $000000FF;
Inc(Vertices);
Vertices.X := -1.0; // Первая вершина квадрата
Vertices.Y := -1.0;
Vertices.Z := 0.0;
Vertices.Color := $00FFFF00;
Inc(Vertices);
Vertices.X := -1.0; // Вторая вершина квадрата
Vertices.Y := 1.0;
Vertices.Z := 0.0;
Vertices.Color := $00FFFF00;
Inc(Vertices);
Vertices.X := 1.0; // Третья вершина квадрата
Vertices.Y := -1.0;
Vertices.Z := 0.0;
Vertices.Color := $00FFFF00;
Inc(Vertices);
Vertices.X := 1.0; // Четвертая вершина квадрата
Vertices.Y := 1.0;
Vertices.Z := 0.0;
Vertices.Color := $00FFFF00;
При каждой перерисовке кадра вызывается процедура:
procedure TfrmD3D.DrawScene;
var
matView, matProj : TDSDMatrix; // Матрицы 4x4
matRotate, matTranslate : TDSDMatrix;
begin
// Получить матрицу поворота вокруг оси X
SetRotateXMatrix(matRotate, Angle); // Матрица сдвига по оси X, на единицу влево
SetTranslateMatrix(matTranslate, -1.0, 0.0, 0.0); // Устанавливаем мировую матрицу трансформаций FDSDDevice.SetTransform(D3DTS_WORLD,
MatrixMul(matRotate, matTranslate)); // Выводится треугольник
FD3DDevice.DrawPrimiti.ve(D3DPTJTRIANGLELIST, 0, 1); // Квадрат вращается по оси Y в 2 раза быстрее треугольника SetRotateYMatrix(matRotate, 2 * Angle); // Квадрат сдвигается на единицу вправо
SetTranslateMatrix(matTranslate, 1.0, 0.0, 0.0); // Матрица трансформаций для квадрата
FD3DDevice.SetTransform(D3DTS_WORLD,
MatrixMul(matTranslate, matRotate)); // Вывод квадрата
FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 3, 2); // Задаем видовую матрицу
SetViewMatrix(matView, D3DVector(0, 0, -5),
D3DVector(0, 0, 0), D3DVector(0, 1, 0)); // Устанавливаем видовую матрицу
FD3DDevice.SetTransform(D3DTS_VIEW, matView); // Задаем матрицу проекций
SetProjectionMatrix(matProj, I, 1, 1, 10); // Устанавливаем матрицу проекций
FD3DDevice.SetTransform(D3DTS_PROJECTION, matProj);
end;
Тип TD3DMatrix, массив 4x4 вещественных чисел, определен в модуле DirectxGraphics, а все функции операций с матрицами - в модуле DXGUtils. Эти функции возвращают величину типа HRESULT, значение которой мы, для простоты, анализировать не будем.
Функция D3DVector этого же модуля возвращает сформированный по трем аргументам вектор, тройку вещественных чисел, величину типа TD3DVector.
Функция SetRotateXMatrix первым аргументом получает переменную, в которую помещается результат, матрицу поворота вокруг оси X. Второй аргумент - угол, в радианах, на который осуществляется поворот. Функция SetTranslateMatrix первым аргументом получает переменную, в которую помещается заполненная матрица сдвига. Одновременно можно сдвинуть по нескольким осям.
Метод setTransform объекта устройства позволяет установить матрицу трансформаций. Первый аргумент - константа, определяющая, для какой матрицы устанавливается трансформация. Второй аргумент - собственно матрица трансформаций. Здесь мы передаем результирующую матрицу, полученную умножением матрицы поворота и матрицы сдвига, но не обязательно, чтобы в трансформации участвовало несколько матриц. Функция MatrixMul позволяет умножить две матрицы, передаваемые в качестве параметров.
Напоминаю, что порядок перечисления этих матриц очень важен. В данном случае разноцветный треугольник поворачивается вокруг оси X, затем сдвигается на единицу влево, по этой же оси.
Квадрат в этом примере вначале сдвигается вправо, затем поворачивается вокруг оси Y (собственной оси, а не мировой). Измените порядок перемножения матриц, чтобы убедиться, что результат будет отличаться от предыдущего.
Функция setviewMatrix подготавливает видовую матрицу. Параметры функции следующие: матрица, в которую помещается результат, вектор, определяющий точку, где располагается голова наблюдателя, опорная точка, определяющая середину видимой области, и вектор, задающий направление взгляда.
Функция setProjectionMatrix предназначена для удобного определения матрицы проекции. Второй аргумент функции задает угол обзора камеры по оси Y, третий аргумент - отношение, определяющее угол обзора по оси X, последние два аргумента - расстояния от глаза наблюдателя до ближней и дальней плоскостей отсечения.
Подозреваю, что последние две функции вызовут много вопросов, поэтому чуть позже мы подробно разберем их смысл. Пока же мы должны только помнить, что смотрим на сцену со стороны оси Z, и находимся от точки отсчета системы координат на расстоянии 5 единиц.
Реалистичные изображения
Для получения реалистичных изображений необходимо выполнить три условия:
- при описании примитивов задать нормали;
- определить свойство материала;
- включить источник света.
Формат вершин теперь помимо пространственных координат обязан включать вектор нормали (тройку вещественных чисел), а FVF-флаг должен дополниться константой D3DFVF_NORMAL. ЭТО первое новшество в модуле нашего следующего примера, проекта каталога Ех02, где рисуется красивый желтый кубик (рис. 9.3).
Рис. 9.3. Наше первое реалистичное изображение
Итак, запись описания вершины дополнилась тремя полями:
type
TCUSTOMVERTEX = packed record
X, Y, Z : Single;
nX, nY, nZ : Single; // Вектор нормали end;
const
D3DEVF_CUSTOMVERTEX = D3DFVF_XYZ or D3DFVF_NORMAL;
Буфер содержит 36 вершин, предназначенных для построения куба. Они образуют 12 независимых треугольников, по 2 соприкасающихся треугольника на каждую сторону куба. Все треугольники описываются по часовой стрелке, чтобы при воспроизведении мы могли, для экономии времени, отключить воспроизведение примитивов, перечисляемых в поле зрения против часовой стрелки. То есть стороны куба, повернутые к нам задней стороной, воспроизводить не будем, это обычный прием, применяемый к замкнутым трехмерным фигурам. Нормали для всех вершин, относящихся к одной стороне, задаются одинаковыми, исходя из того, какая сторона куба описывается. Так выглядит описание первого треугольника:
Vertices.X := -0.5;
Vertices.Y := -0.5;
Vertices.Z := -0.5;
Vertices.nX := -1.0;
Inc(Vertices);
При инициализации графической системы вызывается процедура, задающая свойства материала и включающая источник света:
procedure TfrmD3D.SetupLights;
var
Material : TD3DMaterial8;
Light : TD3DLight8;
begin
// Инициализация материала, желтый цвет
Material := InitMaterial(1, 1, 0, 0) ;
// Устанавливаем материал в объекте устройства
FD3DDevice.SetMaterial(Material);
// Инициализация направленного источника, белый свет
Light := InitDirectionalLight(DSDVector(0, 0, 1), 1, 1, 1, 0) ;
// Устанавливаем источник света
FDSDDevice.SetLight(0, Light);
// Включаем источник света
FD3DDevice.LightEnable(0, True);
end;
Материал и источник света являются записями (не СОМ-объекты) и имеют тип TD3DMateriais и TD3DLight8 соответственно. Пользовательская функция InitMaterial заполняет поля структуры материала и получает в качестве аргументов значения ARGB. Отличает эти параметры от привычного их использования, помимо порядка, в котором они перечисляются, то, что это вещественные числа, единица соответствует максимальному значению аргумента.
В примере материал задается желтым, для того, чтобы установить его. При этом используется метод SetMaterial объекта устройства.
Функция InitDirectionalLight заполняет поля структуры, описывающей направленный источник света. Первым аргументом передается вектор, задающий направление лучей света. Напоминаю, что мы наблюдаем сцену с отрицательной стороны оси Z. Чтобы лучи света были параллельны нашему взору, вектор направления задается (0, 0, 1). Следующие три аргумента описывают цветовой фильтр, накладываемый на источник света, обычно источник задается белым. Эти числа также вещественны. Значение последнего аргумента для направленного источника безразлично.
Метод setLight объекта устройства устанавливает источник света на сцене. Первый аргумент, целое число, основанное на нуле, является индексом, идентификатором источника света. Метод только задает источник света, включается же он с помощью отдельного метода, LightEnabie, первый аргумент которого - индекс нужного источника, второй аргумент - булево выражение.
Как я уже говорил, отключается воспроизведение задних сторон треугольников, т. е. тех, чьи вершины перечисляются против часовой стрелки:
SetRenderState(D3DRS__CULLMODE, D3DCULL_CCW);
Совсем не обязательно, чтобы вершины примитива перечислялись именно по часовой стрелке, можно использовать и противоположное направление. Просто желательно, чтобы существовал какой-нибудь определенный порядок перечисления, чтобы можно было отсекать воспроизведение задних сторон. Повторюсь, внутренние стороны кубика нам не видны в любом случае, поэтому и незачем тратить время на их воспроизведение. Также обращаю ваше внимание на то, что связанные треугольники приспособлены для перечисления вершин именно по часовой стрелке.
Есть и еще один важный аспект, который нам необходимо учитывать: DirectSD не может окрашивать примитивы с двух сторон. Замените последний аргумент метода Drawprimitive на 2 и установите значение для режима D3DRs_CULLMODE в D3DCULL_NONE. Теперь будет выводиться только одна сторона куба, отсечение задней стороны примитивов не производится. Обратите внимание, что когда квадрат поворачивается к зрителю задней стороной, он выводится черным, т. е. совершенно не окрашиваемым.
Кубик в нашем примере вращается вокруг двух осей одновременно:
SetRotateXMatrix(matRotateX, Angle);
SetRotateYMatrix(matRotateY, Angle);
FD3DDevice.SetTransform(D3DTS_WORLD, MatrixMul(matRotateX, matRotateY));
FD3DDevice.DrawPrimitive(D3DPT__TRIANGLELIST, 0, 12);
На рисунке куб получился крупнее, чем при работе приложения. Для того, чтобы увеличить изображение, можно просто "приблизить" глаз наблюдателя:
SetViewMatrixfmatView, D3DVector(0, 0, -2),
D3DVector(0, 0, 0), D3DVector(0, I, 0));
Есть и другой способ: действительно увеличить объект. Для этого в матрицу трансформаций надо добавить матрицу масштабирования, по главной диагонали которой стоят числа, отличные от единицы и равные масштабным множителям по трем осям отдельно. Попробуйте сейчас увеличить кубик в два раза:
procedure TfrmD3D.DrawScene;
var
matView, matProj : TD3DMatrix;
matRotateX, matRotateY : TD3DMatrix;
niatScale : TD3DMatrix; // Добавилась матрица масштабирования
begin
SetRotateXMatrix(matRotateX, Angle);
SetRotateYMatrix(matRotateY, Angle);
SetScaleMatrix(matScale, 2.0, 2.0, 2.0); // Увеличиваем в 2 раза
// Добавляем матрицу масштабирования
FD3DDevice.SetTransform(D3DTS_WORLD, MatrixMul(matScale,
MatrixMul(matRotateX, matRotateY)));
Обязательно это сделайте, чтобы увидеть, что куб действительно увеличился. Однако освещение его тоже изменилось. Связано это с тем, что векторы нормалей к вершинам вслед за масштабированием стали увеличенными, и требуется их нормализация. В таких случаях необходимо включить режим автоматической нормализации этих векторов:
SetRenderState(D3DRS NORMALIZENORMALS, DWORD (True));
